Codes correcteurs d'erreur
généralités sur les codes linéaires

Notre société est devenue dépendante de la communication sous toutes ses formes, notamment les messages numériques dont le volume augmente sans cesse. Il faut donc assurer l'intégrité des données à la réception, malgré des moyens de transmission qui ajoutent parfois des erreurs à l'information : ondes radio, ligne téléphonique, support magnétique, etc. C'est le rôle des codes correcteurs d'erreurs.

Pour une réelle compréhension de la justification et de la mise en œuvre des codes correcteurs, il m'a semblé utile de s'intéresser à la généralité de la grande classe des codes linéaires. On évitera ainsi de se précipiter sur une description admirative et superficielle de codes trop compliqués pour être bien compris dans les limites d'un T.I.P.E.

I.       Cadre de la correction d'erreurs

A.     introduction

S'il n'y avait pas de code correcteur sur un CD audio par exemple, où les erreurs sont dues à des rayures, décalage de la lentille lors de la lecture ou simplement à des défauts de fabrication, il y aurait environ un claquement par seconde dû à une inversion de signe de l'échantillon joué.

Mettre en œuvre un code correcteur consiste à introduire une redondance dans l'information à transmettre. Ceci permet de détecter et éventuellement de corriger les cas où la transmission a modifié le message. Il peut sembler paradoxal de compresser un fichier pour éliminer toute redondance puis d'en réintroduire. Un code correcteur est en fait une redondance réfléchie et optimisée pour minimiser le taux d'erreurs non détectées et la longueur des bits ajoutés.

La détection d'erreur n'est pas toujours suffisante : alors que l'on peut demander la ré-émission d'un paquet corrompu entre deux composants d'un ordinateur (erreurs rares, rapidité prioritaire), les délais de transmission des satellites imposent de pouvoir détecter et corriger les inévitables erreurs. Cela est évident pour le stockage d'information, qui fait aussi partie du cadre de la correction d'erreurs.

B.     canal de transmission

C'est un système physique permettant la transmission d'une information entre deux points distants (dans le temps ou l'espace). Son taux d'erreur binaire est le rapport entre le nombre de bits modifiés et le nombre de bits du message.

1.      canal binaire symétrique

Il est caractérisé par son taux d'erreur p. La probabilité pour un bit 1 d'être modifié en 0 est p, donc celle pour un bit 0 d'être modifié en 1 est p aussi. D'où le nom de « symétrique ».

2.      canal binaire à effacement

On considère ici la possibilité pour un bit d'être effacé, i.e. remplacé par un blanc, par exemple lors d'un brouillage sur une ligne téléphonique (on ne peut plus distinguer les bits reçus) ou d'une brève interruption de lecture de la piste d'un CD. On connaît alors la position de l'erreur, ce qui facilite le décodage.

C.     théorème de Shannon

En 1948, Claude Shannon énonce dans A Mathematical Theory of Information le théorème fondamental de la théorie de l'information :

1.      énoncé

Tout canal de transmission admet un paramètre C, appelé capacité du canal, tel que pour tout e > 0 et pour toutR < C, il existe un code de rendement R permettant la transmission de l'information avec un taux d'erreurs binaire plus petit que e..

En d'autres termes, on peut obtenir des transmissions aussi fiables que l'on veut, à condition d'utiliser des codes de rendement plus petits que la capacité du canal. Cependant, ce théorème n'indique pas le moyen de construire de tels codes.

2.      remarques

La notion de rendement est définie plus loin.

Nous ne traiterons que les codes en bloc (principalement par opposition aux codes convolutifs), c'est à dire découpant l'information en blocs traités séparément. Parmi les codes convolutifs, les turbo codes semblent aujourd'hui s'approcher de cette limite.

II.     Quelques exemples simples

A.     code de répétition

Une première idée intuitive est de transmettre deux fois chaque bit. Si on ne reçoit pas deux fois la même chose, il y a eu une erreur, mais on ne sait pas la corriger. Il faut donc le transmettre trois fois. On pourra ainsi corriger une erreur par groupe de trois bits, mais deux erreurs dans le même groupe conduiront à une interprétation erronée.

B.     code de parité

1.      parité simple

Ce code fréquent consiste simplement à ajouter un bit à la fin de chaque octet : la somme modulo 2 des bits de cet octet. Chaque mot ainsi formé a donc un nombre pair de bits égaux à 1. On détecte une erreur par groupe de huit bits avec ce code.

2.      double parité

Pour pouvoir corriger une erreur, on regroupe les octets par huit. On écrit alors les bits dans un tableau , et on ajoute un bit de parité comme dans le code précédent pour chaque ligne et chaque colonne. S'il y a une erreur, elle est localisée par croisement de la ligne et de la colonne, donc corrigeable.

C.     le plus petit code de Hamming

Soient quatre bits d'information A₃, A₅, A₆, A₇. On calcule les bits de parité P₁, P₂, P₄ comme ci contre. Si i fait intervenir j dans sa décomposition en base 2, alors A_i intervient dans le calcul de P_j. On transmet alors A₇A₆A₅P₄A₃P₂P₁. À la réception on calcule P'_i  de la même façon que P_i. indique l'indice du bit erroné (0 s'il n'y a pas d'erreur). S'il y a plus d'une erreur, elle ne peut pas être corrigée.

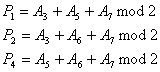
Cette construction est généralisable, on obtient une classe de codes corrigeant une erreur.

III.  Les codes linéaires

A.     définitions

·           information : ce que l'on désire transmettre, donc l'entrée de l'algorithme de codage.

·           message : ce qui est effectivement transmis, donc la sortie de l'algorithme de codage.

·           caractère : constituant élémentaire de l'information et du message. L'ensemble des caractères est un alphabet fini A. A est en corps dans toute la suite, Z/2Z lorsque l'on travaille sur des bits.

·           code en bloc : plongement de A^k dans Aⁿ.

C'est à dire qu'un bloc d'information de k caractères sera codé par un mot de n caractères. On appelle alors n la longueur du code et k/n son rendement. On peut oublier (le temps de l'étude) la correspondance entre l'information et son codage, et considérer simplement l'image de cette injection, c'est une partie de Aⁿ.

·           code linéaire : sous espace vectoriel de Aⁿ. k est donc la dimension du code. On n'étudiera ici que les codes linéaires, les plus utilisés aujourd'hui. Cette contrainte sur la structure du code permet d'utiliser les résultats d'algèbre linéaire et de faciliter ainsi codage et décodage pour des codes longs. Peu de méthodes existent pour rechercher de bons codes non linéaires.

·           poids d'un mot : nombre de coordonnées non nulles.

·           distance de Hamming : nombre de coordonnées différentes entre deux vecteurs (ou mots) de Aⁿ. d(a, b) est donc le poids de a-b. Cette distance vérifie d(a, b) = d(a-c, b-c) pour tous vecteurs a, b, c.

·           distance minimale d d'un code : minimum des distances entre deux mots du code. Puisque le code est linéaire, c'est le minimum des distances au vecteur nul, ou encore le poids minimum d'un mot non nul.

Cette notion est fondamentale, elle mesure la capacité de correction d'un code. En effet si 2e<d, alors le code peut corriger e erreurs. (En effet si et sont deux mots du code à distance inférieure ou égale à e du message reçu, alors donc ). On peut montrer de même que si 2t + e < d, alors le code peut corriger e erreurs et t effacements.

·           paramètres d'un code : (n, k, d) avec les notations précédentes.

B.     description matricielle des codes linéaires binaires

Ici l'alphabet est A = Z/2Z.

1.      matrice génératrice G

On peut remarquer que dans le code de Hamming, le calcul du vecteur (A₇A₆A₅P₄A₃P₂P₁) à partir de (A₇A₆A₅A₃) est une application linéaire dont la matrice est la transposée de la matrice ci contre. Cette construction est générale : soit v₁, ..., v_k une base de l'espace vectoriel qu'est le code, la concaténation de ces vecteurs est une matrice de taille génératrice du code. L'opération de codage est alors simplement l'application linéaire définie par cette matrice.

2.      matrice de parité H

On définit de façon canonique le produit scalaire de deux mots a et b de (Z/2Z)ⁿ par . C'est de façon équivalente le poids du produit bit à bit de a et b. On notera qu'il existe des vecteurs orthogonaux à eux-mêmes, on devrait donc parler seulement d'une forme bilinéaire symétrique. Si est un code de dimension k, son orthogonal  est de dimension n-k comme intersection de k formes linéaires indépendantes. Soit v₁, ..., v_n-k une base de , la concaténation de ces vecteurs est la matrice de parité H. c est un mot du code si et seulement si ^tcH=0, d'où la relation ^tGH=0. L'algorithme de décodage utilisé en annexe est basé sur ces considérations.

3.      forme systématique

Deux codes sont dits équivalents s'ils ne diffèrent que d'une permutation de leurs composantes, c'est à dire si leur matrices génératrices sont identiques à une permutation de lignes près. Par un pivot de Gauss, on peut donc imposer en toute généralité que les k premières lignes de G constituent la matrice identité. Si P est la matrice constituée des n-k dernières lignes de , on peut prendre .

C.     majoration de d

1.      d'après la forme de H

Si H possède w lignes dépendantes, on peut exprimer la combinaison linéaire (nulle) de ces lignes par le vecteur ^tcH, où c_i = 1 si et seulement si la i^ème ligne de H fait partie de cette combinaison linéaire. Ainsi c fait partie du code, a un poids w, donc d est majoré par w. La réciproque est analogue, ainsi d est le nombre minimum d'éléments d'une combinaison linéaire nulle non triviale de lignes de H. Il existe une telle combinaison car H a n lignes de longueur n-k.

2.      Singleton

d est majoré par n-k+1. En effet, le sous espace vectoriel composé des vecteurs ayant leurs k-1 dernières composantes nulles est de dimension n-k+1 donc contient un mot du code. Le poids de ce mot est majoré par n-k+1.

3.      combinatoire

On revient au cas général pour A, et on pose q son cardinal.

Soit t la partie entière de (d-1)/2. Les boules centrées sur un mot du code sont disjointes, et contiennent chacune éléments. Il y en a q^k donc 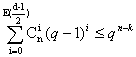. On dit qu'un code est parfait s'il réalise l'égalité : les boules ci dessus sont une partition de Aⁿ, il n'y a pas de « place perdue ».

D.     décodage

Tout algorithme est basé sur le fait qu'il est plus probable qu'il y ait eu peu d'erreurs que beaucoup. On cherche donc le mot du code le plus proche du mot reçu. Ils doivent être efficaces, donc plus élaborés qu'une recherche exhaustive du mot de code le plus proche ou que celui décrit en annexe. Ils sont trop complexes pour être pleinement compris en cinq pages.

Le décodage est la partie la plus complexe de la mise en œuvre d'un code. Des améliorations sont parfois proposées longtemps après la mise au point d'un algorithme de codage. C'est pourquoi les codes utilisés sont souvent loin des différentes limites exposées.

IV. Améliorations d'un code

A.     Entrelacement

Les erreurs arrivent souvent par paquets : rayure sur un cédérom, bruit bref sur une ligne de téléphone, etc. Or un message dont beaucoup de mots contiennent chacun peu d'erreurs peut être corrigé, contrairement à un message dont quelques mots contiennent beaucoup d'erreurs. D'où l'idée de mélanger les caractères du message, de manière à répartir les erreurs : deux caractères proches se retrouvent éloignés après l'entrelacement.

1.      par grille

On écrit la suite de caractères de l'information dans un tableau de taille m*n, ligne par ligne. On le relit alors colonne par colonne. L'élément d'indice est donc à la position dans le message. Mais cette méthode ne garantit pas d'éloignement minimum entre deux caractères consécutifs du message.

2.      continu

Exemple : on écrit les caractères dans cet ordre :

et on les relit colonne par colonne : 1, *, *, 2, 6, *, 3, 7, 11, 4, 8, 12, 5, 9, 13 ,16, 10, 14, 17, 21, 15, 18, 22, 26, ...

Plus il y a de lignes dans le tableau, plus deux éléments consécutifs sont éloignés.

B.     codes en série

On utilise souvent plusieurs codes en série : la sortie de l'un est l'entrée de l'autre. Avec un entrelacement entre les deux codes, les performances sont grandement améliorées. En effet lorsqu'un mot ne peut être corrigé par le premier code, ce mot mal corrigé sera réparti en plusieurs erreurs isolées pour le second, qui les corrigera.

C.     valeurs souples

Cela consiste simplement à perfectionner le démodulateur physique pour qu'il ne fasse plus de décision dure sur un bit reçu, mais donne une probabilité pour que le bit soit bien celui annoncé. Le décodage s'en trouve bien sûr compliqué, mais les performances améliorées.

Cela s'applique également pour des codes en série : le premier décodage donne une probabilité d'autant plus faible que le nombre d'erreurs corrigées dans le bloc est grand. Après désentrelacement, le deuxième décodeur tient compte des bits les plus vraisemblables.

D.     pour le CD audio

On sait de plus que l'information représente de la musique. En cas d'erreur non corrigée mais détectée, on peut interpoler (en minimisant une certaine énergie) le signal entre deux échantillons connus, et éviter ainsi un claquement dans les enceintes. L'entrelacement est particulièrement utile ici puisqu'on ne peut interpoler sur de trop longues durées.

V.   Annexes

A.     comparaison des codes

À rendement égal, un code est d'autant plus efficace qu'il est long. En effet le code naïf corrigeant une erreur sur trois bits ne fonctionne que si les erreurs sont bien réparties. Un code de paramètres (300,100,201) corrigera 100 erreurs sur 300 bits quelles que soient leurs positions.

2.      taux d'erreur : 0.42

Pour illustrer un effet pervers : si le taux d'erreur est trop grand, le code ajoute des erreurs.

3.      taux d'erreur : 0.01

Presque aucun canal n'est autant bruité dans la réalité. Le code de Golay réalise une correction presque parfaite.

B.     extraits du code source Caml

J'ai écrit ce code afin de réaliser les illustrations précédentes. Je n'en donne ici que les fonctions intéressantes, on ne trouvera pas par exemple l'implémentation mat_prod du produit matriciel.

1.      encodage

(*On calcule la matrice génératrice à partir de la matrice de parité sous forme systématique, puis on renvoie l'application linéaire.*)

let encode mat_parité =
let n = vect_length mat_parité.(0) in
let k = n - vect_length mat_parité in
let mat_génératrice = make_matrix k n false in
for i=0 to k-1 do mat_génératrice.(i).(i) <- true done;
for i=0 to k-1 do
  for j=k to n-1 do
    mat_génératrice.(i).(j) <- mat_parité.(j-k).(i)
  done
done;
fun données -> (mat_prod [|données|] mat_génératrice).(0);;
(*On code les mots comme des vecteurs ligne, et on utilise donc les transposées des matrices décrites plus haut.*)

2.      décodage

(*On établit la table de l'erreur la plus probable en fonction du syndrome, puis on renvoie la fonction qui décode.*)

let décode mat_parité =
let n = vect_length mat_parité.(0) in
let nmk = vect_length mat_parité in (*n moins k*)
let th = transpose mat_parité in
let table = ref (empty compare) in
let nouveau syndrome =
  try let _ = find syndrome !table in false
  with Not_found -> true in
let erreur = make_vect n false in
let i = ref 0 in
let borne = 1 lsl nmk in (*borne = 2^(n-k)*)
while !i < borne do
  let syndrome = (mat_prod [|erreur|] th).(0) in
  if nouveau syndrome
    then (incr i; table := add syndrome (copy_vect erreur) !table);
  pos_suivante erreur;
done;
let table = !table in
fun information -> (*enfin !*)
  let syndrome = (mat_prod [|information|] th).(0) in
  let erreur = find syndrome table in
  init_vect (n-nmk) (fun i -> information.(i) xor erreur.(i));;

3.      matrices de parité

let convert = map_vect (map_vect (prefix = 1));; (*convertit les 0/1 en false/true : la matrice de parité est plus lisible dans le code source ainsi.*)

let hamming3 = convert
[|[|1;1;1;0;1;0;0|];
  [|1;1;0;1;0;1;0|];
  [|1;0;1;1;0;0;1|]|];;

let naïf = convert
[|[|1;1;0|];
  [|1;0;1|]|];;

let BCH1575 = convert
[|[|1;1;0;1;0;0;0;1;0;0;0;0;0;0;0|];
  [|0;1;1;0;1;0;0;0;1;0;0;0;0;0;0|];
  [|0;0;1;1;0;1;0;0;0;1;0;0;0;0;0|];
  [|0;0;0;1;1;0;1;0;0;0;1;0;0;0;0|];
  [|1;1;0;1;1;1;0;0;0;0;0;1;0;0;0|];
  [|0;1;1;0;1;1;1;0;0;0;0;0;1;0;0|];
  [|1;1;1;0;0;1;1;0;0;0;0;0;0;1;0|];
  [|1;0;1;0;0;0;1;0;0;0;0;0;0;0;1|]|];;

let double_parité = convert
[|[|1;1;1;0;0;0;0;0;0;1;0;0;0;0;0;0|];
  [|0;0;0;1;1;1;0;0;0;0;1;0;0;0;0;0|];
  [|0;0;0;0;0;0;1;1;1;0;0;1;0;0;0;0|];
  [|1;0;0;1;0;0;1;0;0;0;0;0;1;0;0;0|];
  [|0;1;0;0;1;0;0;1;0;0;0;0;0;1;0;0|];
  [|0;0;1;0;0;1;0;0;1;0;0;0;0;0;1;0|];
  [|1;1;1;1;1;1;1;1;1;0;0;0;0;0;0;1|]|];;

let golay = convert (*23,12,7*)
[|[|1;0;1;0;0;0;1;1;1;0;1;1;1;0;0;0;0;0;0;0;0;0;0|];
  [|1;1;0;1;0;0;0;1;1;1;0;1;0;1;0;0;0;0;0;0;0;0;0|];
  [|0;1;1;0;1;0;0;0;1;1;1;1;0;0;1;0;0;0;0;0;0;0;0|];
  [|1;0;1;1;0;1;0;0;0;1;1;1;0;0;0;1;0;0;0;0;0;0;0|];
  [|1;1;0;1;1;0;1;0;0;0;1;1;0;0;0;0;1;0;0;0;0;0;0|];
  [|1;1;1;0;1;1;0;1;0;0;0;1;0;0;0;0;0;1;0;0;0;0;0|];
  [|0;1;1;1;0;1;1;0;1;0;0;1;0;0;0;0;0;0;1;0;0;0;0|];
  [|0;0;1;1;1;0;1;1;0;1;0;1;0;0;0;0;0;0;0;1;0;0;0|];
  [|0;0;0;1;1;1;0;1;1;0;1;1;0;0;0;0;0;0;0;0;1;0;0|];
  [|1;0;0;0;1;1;1;0;1;1;0;1;0;0;0;0;0;0;0;0;0;1;0|];
  [|0;1;0;0;0;1;1;1;0;1;1;1;0;0;0;0;0;0;0;0;0;0;1|]|];;

4.      nombre d'erreurs corrigées

(*exécute test sur les 2^n vecteurs booléens de taille n
  ici on fourni à test le nombre d'éléments égaux à true du vecteur à tester*)

let teste test n =
let nb_true = ref 0 in
let rec gray t i = (*essais exhaustifs dans l'ordre du code de gray*)
if i>=0 then
 (gray t (i-1);
  let b = t.(i) in t.(i) <- not b;
  (if b then decr else incr) nb_true;
  test t !nb_true;
  gray t (i-1);
 ) in
let t = make_vect n false in
test t 0; gray t (n-1);;

let stats décodeur k n =
let corrigées = make_vect (n+1) 0 in
  (*nombre d'erreurs corrigées en fonction du poids*)
let nul_vect = make_vect k false in
let test t poids =
  if décodeur t = nul_vect then corrigées.(poids) <- corrigées.(poids) +1 in
teste test n;

corrigées;;

(*résultats :
  #stats (décode naïf) 1 3;;
  - : int vect = [|1; 3; 0; 0|]

  #stats (décode hamming3) 4 7;;
  - : int vect = [|1; 7; 0; 0; 0; 0; 0; 0|]

  #stats (décode BCH1575) 7 15;;
  - : int vect = [|1; 15; 105; 135; 0; 0; 0; 0; 0; 0; 0; 0; 0; 0; 0; 0|]

  #stats (décode double_parité) 9 16;;
  - : int vect = [|1; 16; 48; 48; 15; 0; 0; 0; 0; 0; 0; 0; 0; 0; 0; 0; 0|]

  #stats (décode golay) 12 23;;
  - : int vect = [|1; 23; 253; 1771; 0; 0; 0; 0; 0; 0; 0; 0; 0; 0; 0; 0; 0; 0; 0; 0; 0; 0; 0; 0|]*)

Commentaires : les codes naïf, hamming3 et golay corrigent comme promis jusqu'à (d-1)/2 erreurs. Le code BCH (15,7,5) corrige en plus 135 des 455 possibilités de 3 erreurs. De même, le code double_parité corrige certaines erreurs bien réparties. Il s'agit de décodeurs complets : ils donnent systématiquement le mot de code le plus vraisemblable. On utilise plutôt aujourd'hui des décodeurs incomplets : si la distance entre mot reçu et mot de code le plus proche est trop grande, le décodeur renvoie un effacement au lieu d'un mot de code douteux. Avec un entrelacement, un autre code en série pourra ainsi corriger plus souvent le mot très perturbé.

C.     Bibliographie

1.      sources principales

M Demazure, Cours d'algèbre : primalité, divisibilité, codes, Cassini, 1997
Gérard Battail, Théorie du codage et protections contre les erreurs, Techniques de l'Ingénieur E170
Olivier Pothier, Codage de canal et turbo codes (était sur la page www.comelec.enst.fr/~pothier/ qui a disparu)
G. Lachaud, S. Vladut, Les codes correcteurs d'erreurs, La Recherche n°278, pp. 778-782, 1995

2.      pour approfondir

E. Shannon, A Mathematical Theory of Communication, The Bell System Technical Journal, vol. 27, pp. 379-423, 623-656, 1948
D.G. Hoffman et coauteurs, Coding theory, The essentials, Marcel Dekker Inc, 1992
F.J. Mac Williams et J.J.A. Sloane, The theory of error correcting codes, North-Holland, 1977
R.J. Mac Eliece, The Theory of information and coding, Addison-Wesley, 1977
S.A. Vanstone et P.C. Oorschot, An introduction to error correcting codes with applications, Kluwer Academic Publisher, 1990

L'information est la richesse d'une société.
Elle exige stockage et transmission fiables.